________________________________________________________________

03.06.1932, Noether an Hasse

Inhalt:

Ein Lemma über verschränkte Produkte. Lokale Klassenkörpertheorie. Chevalleys Brief. Nicht-galoissche Zerfällungskörper. Noethers Gauß-Lektüre.

Göttingen, 2./3. 6. 1932

Lieber Herr Hasse!

Ihr hübscher Satz macht mir viel Vergnügen; vor allem aber die Tatsache, daß damit im Kleinen der Übergang vom zyklischen zum abelschen geht. Damit wird doch vielleicht die Rolle der Normen im abelschen geklärt, was ja durch Faktorensyst[eme] allein nicht geht.¹⁾ Können Sie mir leihweise die Mitteilung von Chevalley schicken? Sie bekommen sie bald wieder! ²⁾

Ich kann den Satz, den ich mir selbst nicht überlegt hatte, mit verschränkter Darstellung beweisen und verallgemeinern (S. 190 Ihrer amerikanischen Arbeit); mit den u_S als Basis des Darstellungsmoduls.³⁾ So hatte ich mir auch die Artinschen Beweise zurechtgelegt; habe ich Ihnen das nicht von Breslau aus geschrieben oder angedeutet? Übrigens hat mir R. Brauer schon vor Jahren erzählt, daß man Aⁿ ~ 1 aus den Assoziativrelationen folgern kann (“zuerst” von Artin bemerkt, stimmt also nicht); es steht in einer der jetzt erscheinenden Crelle-Arbeiten.⁴⁾

Die verschränkte Darstellung ist deshalb einfacher, weil die Assoziativrelationen in der trivialen Form “(u_Su_R)u_T = u_S(u_Ru_T)” benutzt werden, um den Modul als Darstellungsmodul zu charakterisieren, nicht in der komplizierten auf Faktorensysteme umgeschriebenen. Sonst läuft alles Ihrem Beweis parallel.⁵⁾

Sei also: A = (KL×× G;a,b,c) mit G = S × T.

Ich betrachte die Reihe der verschränkten Darstellungen und “verallgemeinerten” verschr[änkten] Darstellungen mit r = (...,u_R,...), wo R alle Elemente S aus S durchläuft.

1) u u-= u -a -; S S ( SS S,S ruS =-r aR(,S)PS), wo(PS d)ie Permutation R --> RS-bedeutet. ruSu S = r aR,S P SaR,S PS = ruSSaS,S = r(aR,SS)PSSaS,S ; also durch ¨Ubergang zu Determinanten (das ist hier rein multiplikativ, also auch im Artinschen Fall m¨oglich, wo die aS,S-Ideale; Schursche Umformung der Hauptidealbedingung): prod anS,S = ASA-SS/ASS-mit AS = R(aR,S); also an-~ 1. 2) u u S,=Su u b (die Reziproken Ihrer b , was bequemer ist) S T T S S,T S,T a) ru = u r(b ); b) ruT u =Tu Rr(,Tb )u = u ru (bS ) = u r(a )P (bS ); aTndeSrerseitTs R,T S T S R,T T R,S S R,T g) = ruSuT b-1 = r(aR,S)PSuTb-1 = ruT(aT )PSb-1 S,T T -1 S,T R,S S,T = uTr(bR,T)(aR,S)PSbS,T; somnit dur1c-hS U¨beTr-g1ang zur Dete prod rminante (rein multiplikativ): bS,T = BT A S mit BT = R bR,T. 3) uTuT* = uT T*cT,T*. Unter Benutzung von 2)a) (und 1) kommt: ruT uT* = uTr(bR,T)uT* = uTuT*r(bR,T*)(bTR*,T) = uT T*cT,T*r(bR,T*)(bT* ) = uTT*r(cR *)(bR,T*)(bT* ); anderseits R,T T,T R,T ruTT *cT,T* = uTT *r(bR,TT*)cT,T *, somit Determin[anten- ]¨Ubergang: cn * = BT *BT*/BT T*.CT,T* mit CT,T* = prod (cR *). T,T T R T,T

Setzt man also: Aⁿ = (u_S,u_T,KL,aⁿ,bⁿ,cⁿ) und weiter: U_S = U_SA_S; U_T = U_TB_T, so kommt: Aⁿ = (U_S,U_T;KL,1,1,C_T,T^*), w.z.b.w.

Der Beweis hat den Vorteil, sich fast ungeändert auf den allgemeineren Fall zu übertragen, wo es sich um galoisschen Unterkörper L von K (anstelle von KL gesetzt) handelt.⁶⁾

Sei nämlich L zum Normalteiler S von G gehörig; sei gesetzt: G = sum _TTS = sum _TST (mit T Repräsentanten d. Restklassen); dann gehen die definierenden Relationen aus 1), 2), 3) über in

1') u u-= u -; ' S S SS -1 2') uSuT = uTuSTbS,T, wo ST = T *ST; * 3 ) uTuT* =* u(TT*)u*ST,T*, wo (TT ) den Repr¨asentanten von T T S bedeutet, also T T = (T T )ST,T*. 4') uTS = uT uS (immer mo¨gliche Normierung), also nach 3'): uTuT* = uT T*cT,T*!

Jetzt bleibt Teil 1) des Beweises wörtlich erhalten, bei Teil 2) wird b_R,T durch (b_R,T)P_T ersetzt, wo P_T die Permutation R '--->

T^-1RT bedeutet; bei Determinantenbildung hebt sich das im Zähler und Nenner auf; Teil 2) bleibt also auch erhalten.
Bei Teil 3) kommt erst die Bemerkung, daß sich die den Relationen 2') entsprechenden für jedes Element D aus G berechnen lassen:

-' 2 ) uSuD = uDuSbS,D;

man hat nur D = T ^.S mit geeigneten T und S zu setzen, was eindeutig ist; dann ergibt sich b_S,D eindeutig: und es kommt, entsprechend 2) oben (denn D kann genauso gut als Repräsentant gewählt werden wie T):

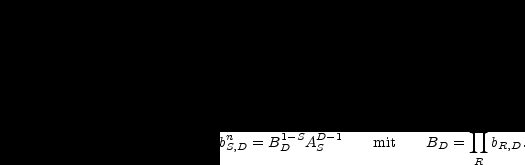
prod bnS,D = B1D-SADS-1 mit BD = bR,D. R

Jetzt bleibt aber 3'), unter Zugrundelegung von u_Tu_T^* = u_TT^*c_T,T^*, bis auf zusätzliche, sich bei Determinantenbildung forthebende Permutationsmatrizen erhalten; also gilt tatsächlich:

prod An = (L,S, cRT,T *); R

da bei Einführung von U_S = U_SA_S, U_T = U_TB_T, allgem. U_TS = U_TSB_TS alle a_S,Sⁿ und b_S,Dⁿ mit beliebigem D sich in assoziierte 1 verwandeln; woraus nach allgemeinen - nicht auf direkte Produkte beschränkten Sätzen die Abspaltung des Einsfaktors folgt (es sind die Sätze, die ich zur Führerbestimmung verwende, die wohl irrational schon bei R. Brauer stehen; Ztschr. 29 glaube ich). Die neuen U_TS sind dabei für T

E, S

E im allgemeinen nicht mehr normiert, was natürlich nichts ausmacht; ich blieb aber erst daran hängen.

Ich halte es nicht für ausgeschlossen daß man vermöge dieser Verallgemeinerungen von der zykl[ischen] Klassenkörperth[eorie] im Kleinen auf das Verhalten der auflösbaren p-adischen Körper schließen kann, also auf das Verhalten der galoisschen Körper im Kleinen, wenn auch wahrscheinlich nur unvollständig. Deshalb interessiert mich natürlich der Übergang von Chevalley! ⁷⁾

Weiter scheint mir die Vereinfachung durch die verschränkte Darstellung es nahe zu legen, auch bei der Erweiterung von Gruppen, bezw. beim Hauptidealsatz, mit verschränkter Darstellung der Gruppen durch den Normalteiler, statt mit den unübersichtlichen Assoziativrelationen zu arbeiten.⁸⁾ Vielleicht bekomme ich einmal jemand dazu!

Einem noch nicht sehr selbständigen Studenten, der sich einarbeiten wollte, habe ich vorgeschlagen, das verschränkte Produkt bei nicht galoisschem Zerfällungskörper einmal explizit anzugeben, durch Einbettung in den zugehörigen galoisschen und Abspalten einer Eins-Algebra. Ich sehe ziemlich wie das laufen muß, hoffe daß er durchhält; andere haben es aufgegeben, da wußte ich aber selbst nichts.⁹⁾

Im übrigen habe ich anläßlich der Ausarbeitung meines Züricher Vortrags¹⁰⁾ einmal Gauß gelesen. Es wurde behauptet, daß ein halbwegs gebildeter Mathematiker den Gaußschen Hauptgeschlechtssatz kennt, aber nur Ausnahmemenschen den der Klassenkörpertheorie. Ob das stimmt, weiß ich nicht - meine Kenntnisse gingen in umgekehrter Reihenfolge - aber jedenfalls habe ich in bezug auf Auffassung allerhand von Gauß gelernt; vor allem daß es gut ist den Nachweis, daß die durch Faktorensysteme bestimmte Klasseneinteilung eine Strahlkl[assen]-Einteilung ist, an den Schluß zu stellen; der Übergang meiner Fassung zu der Gaußschen geht nämlich unabhängig davon direkt, erst die Spezialisierung auf die Klassenkörpertheorie braucht den Führer. Was ich mache, ist die Verallgemeinerung der Definition der Geschlechter durch Charaktere.

Wie ich höre sind Sie bei der Math[ematischen] Gesellschaft vorgemeldet. Ich rechne also sicher damit daß Sie diesen Sommer kommen.¹¹⁾ Ich habe Anfang Mai in Halle vorgetragen; war dann noch in Leipzig. Deuring hat neulich in Erlangen vorgetragen; außerdem in Halle gleichzeitig mit mir.¹²⁾

Also auf Wiedersehen und beste Grüße!

Ihre Emmy Noether.

Anmerkungen zum Dokument vom 3.6.1932

¹In dem Tagebuch von Hasse findet sich unter der Datumsangabe “Mai 1932” ein Eintrag mit dem Titel: “Ein Satz über verschränkte Produkte.” Der dort bewiesene Satz stimmt überein mit demjenigen Satz, den Noether weiter unten beweist. Es ist also anzunehmen, dass Hasse diesen Satz an Noether geschickt hatte, und dass Noether nun ihre Version des Beweises mitteilt. Es handelt sich um einen Hilfssatz über Faktorensysteme, der zum Aufbau der lokalen Klassenkörpertheorie benutzt wurde. Hasse hatte in seiner Annalenarbeit Has:1933 , welche er Noether zum 50. Geburtstag am 23. März 1932 gewidmet hatte, das Normsymbol mit Hilfe von Invarianten von Algebren definiert, jedoch nur für zyklische Erweiterungen. Für diese konnte er mit Hilfe des Normsymbols nachweisen, dass die Normfaktorgruppe isomorph auf die Galoisgruppe abgebildet wird. Es geht jetzt darum, ausgehend von dem zyklischen Fall auch beliebige abelsche Erweiterungen zu behandeln. Das meint Noether, wenn sie schreibt, dass dadurch “die Rolle der Normen im abelschen geklärt” werde. Vgl. Anmerkung 11 zum Brief ^* vom 25.6.1930.

²In dem Nachlass von Hasse findet sich unter dem Datum vom 12. Mai 1932 ein Brief von Chevalley in dem sich ebenfalls eine Mitteilung über den in Rede stehenden Satz befindet. Chevalley schreibt dazu: “J’ai eu la même idée que vous en ce qui concerne les systèmes de facteurs.” Es scheint also, dass Hasse und Chevalley diesen Satz gleichzeitig gefunden hatten. Offenbar will Noether zusätzlich zum Hasseschen Beweis auch den Beweis von Chevalley sehen. Der Satz findet sich dann (als “Lemme 5”) in der Arbeit von Chevalley im Crelleschen Journal Che:1933 . Übrigens verweist Hasse in seiner Tagebucheintragung noch auf einen späteren Eintrag, datiert November 1934, in dem er einen besonders einfachen Beweis dieses Satzes, der von Witt stammt, notiert. Der Wittsche Beweis wurde dann ebenfalls im Crelleschen Journal publiziert Wit:1935 .

³Der Verweis auf die amerikanische Arbeit von Hasse Has:1932 bedeutet nur, dass Noether dieselbe Methode anwendet, die dort auch von Hasse angewandt wird.

⁴Es handelt sich um den Satz, dass die n-te Potenz eines Faktorensystems zerfällt, wenn n die Ordnung der zugrundeliegenden Gruppe G ist. Das wird von Artin in einem Brief an Hasse (9. 3. 1932) als Nebenergebnis vorgerechnet; da Hasse die Artinschen Briefe an Noether geschickt hatte, so war Noether darüber informiert. Für Algebren war der Satz tatsächlich schon lange bekannt. Die Artinschen Rechnungen sind jedoch für Faktorensysteme in einem beliebigen G-Modul gültig: das hatte wohl Hasse gemeint, als er schrieb, dass dies zuerst von Artin bemerkt wurde. - Wir sehen auch an diesem Beispiel das erwachende Bewusstsein für die formalen Regeln der Kohomologietheorie.

⁵Um die folgenden Rechnungen verständlich zu machen, seien einige Erläuterungen vorangestellt: Gegeben seien zwei linear disjunkte Galois-Erweiterungen K|k, L|k eines gemeinsamen Grundkörpers k (der bei Noether nicht gesondert benannt wird). Die Galoisgruppen seien S bezw. T. Die Galoisgruppe des Kompositums KL ist dann G = S × T. Man betrachte eine Algebra A, die gegeben ist als verschränktes Produkt von KL mit G. Das Faktorensystem wird mit a,b,c bezeichnet, wobei a aus denjenigen Faktoren a_S,S^* besteht, deren Indizes S,S^* in S liegen, also die Restriktion des Faktorensystems auf die Untergruppe S. Entsprechend ist c die Restriktion auf T, und b besteht aus den “gemischten” Faktoren b_S,T, b_T,S mit S S und T T. Sei n die Ordnung von S. Der zu beweisende Satz besagt nun, dass Aⁿ ähnlich ist zu einer Algebra B, welche verschränktes Produkt von L|k mit T mit dem Faktorensystem c^N_S ist, wobei N_S = sum _SSS den Normoperator KL --> L bedeutet.

Dieser Satz ist also das bereits in Fußnote 2 zitierte “Lemme 5” von Chevalley. Es wird in Chevalley’s Arbeit Che:1933 benutzt um das Hassesche Normsymbol für beliebige abelsche Erweiterungen eines lokalen Körpers zu definieren, ausgehend von der Hasseschen Definition in Has:1933 für zyklische Erweiterungen. Damit ergibt sich dann die lokale Klassenkörpertheorie, so wie es Noether vorausgesehen hatte.

⁶Diese Verallgemeinerung stimmt so nicht; offenbar wurde Noether von Hasse darauf aufmerksam gemacht, und sie hat das dann in ihrer nächsten Postkarte ^* vom 24. 6. 32 zurückgezogen. - Heute wissen wir aus der Kohomologietheorie folgendes: Ist L|k eine Teilerweiterung der Galois-Erweiterung K|k, so liefert die Verlagerung eine Abbildung ver:H²(K|L) --> H²(K|k). Verbindet man sie mit der Restriktionsabbildung res: H²(K|k) --> H²(K|L) so gilt: ver o res = n (Multiplikation mit n, bezw. Potenzierung mit n bei multiplikativer Schreibweise). Im Spezialfall aber, wenn S Normalteiler von G ist und G über S zerfällt (z.Bsp. wenn S direkter Faktor von G ist), dann lässt sich die Verlagerungsabbildung als “Norm” darstellen, wie es Noether tut.

⁷Vgl. Anmerkung 2.

⁸Jedes Faktorensystem definiert eine Gruppenerweiterung. Anscheinend ist es das, was Noether im Auge hat, wenn sie von einer “verschränkten Darstellung” spricht.

⁹Es handelt sich um den Studenten Werner Vorbeck. Er hat 1935 in Göttingen promoviert mit einer Arbeit mit dem Titel “Nichtgaloissche Zerfällungskörper einfacher Systeme”. Zu dem damaligen Zeitpunkt war Noether bereits aus Göttingen vertrieben, daher agierte F. K. Schmidt formal als Referent. Er stützte sich dabei auf ein Gutachten, dass ihm Noether aus USA geschickt hatte. Obwohl die Arbeit als für eine Promotion ausreichend befunden wurde, scheint Emmy Noether nicht sehr davon begeistert gewesen zu sein, offenbar hatte der Kandidat das vorgegebene Ziel nicht zu ihrer vollen Zufriedenheit erreicht. Die Arbeit wurde zwar in dem “Jahrbuch über die Fortschritte der Mathematik” referiert, jedoch nicht in einer mathematischen Zeitschrift publiziert. Das Thema geriet in Vergessenheit, bis Amitsur die heute sogenannte “Amitsur-Kohomologie” einführte und auf Algebren anwendete.

¹⁰Emmy Noether war eingeladen worden, auf der Züricher Tagung der Internationalen Mathematischen Union im September 1932 einen Hauptvortrag zu halten. Ihr Vortrag hatte den Titel: “Hyperkomplexe Systeme in ihren Beziehungen zur kommutativen Algebra und zur Zahlentheorie” Noe:1932 .

¹¹Hasse trug zwar im Sommer in Göttingen vor, jedoch nicht in der Mathematischen Gesellschaft sondern im Seminar von Emmy Noether. Erst später, nämlich im Januar 1933, kam ein Vortrag von Hasse in der Göttinger Mathematischen Gesellschaft zustande.

¹²In Halle wirkte seit 1930 Heinrich Brandt, auf den die “Brandtschen Gruppoide” zurückgehen; sie dienen zur Beschreibung der Idealtheorie in den Maximalordnungen einer einfachen Algebra. In Leipzig wirkte van der Waerden, mit dem Noether in engem Kontakt stand; van der Waerdens Assistent war damals Deuring (Noethers “Lieblingsschüler”). In Erlangen waren Wolfgang Krull und F. K. Schmidt. - Über Noethers Vorträge in Halle und ihre darauf bezügliche Korrespondenz mit Brandt wird in Jen:1986 berichtet.