________________________________________________________________
06.10.1927, Hasse an Noether
Inhalt:
H.s Antwort: Konstruktion solcher Körper mit Hilfe des Lokal-Global-Prinzips für
quadratische Formen.
Lösung der E. Noetherschen Halle, den 6. 10.
27
Frage auf Karte vom 4. X. 27
Liebe Fräulein Noether!
Ihre Vermutung ist richtig, wenn auch nicht direkte Folge aus meinen früheren
Existenzsätzen. Ich beweise sie aber mit ganz ähnlichen Methoden:
I. Der zu konstruierende Körper vom Grade 2n, zyklisch über dem rationalen
Körper R, heiße k ; sein reell geforderter Unterkörper vom Grade 2n-1 heiße k' . Ich
konstruiere k als den Unterkörper 2n-ten Grades eines Kreiskörpers kp der p-ten
Einheitswurzeln. Damit k selbst imaginär wird, wie es die weitere Forderung
-1 =  12 +
12 +  22 +
22 +  32 in k notwendig bedingt, muß p- 1 genau durch 2n teilbar sein.
Dann ist ersichtlich auch immer k imaginär und k' reell, letzteres weil k' im
Unterkörper
32 in k notwendig bedingt, muß p- 1 genau durch 2n teilbar sein.
Dann ist ersichtlich auch immer k imaginär und k' reell, letzteres weil k' im
Unterkörper  -ten Grades kp' von k
p enthalten ist. Es ist somit zuerst eine
Primzahl p so zu bestimmen, daß
-ten Grades kp' von k
p enthalten ist. Es ist somit zuerst eine
Primzahl p so zu bestimmen, daß
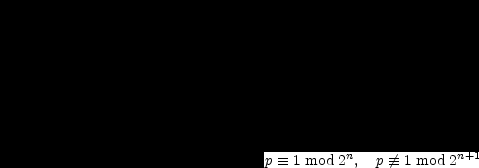 | (1) |
wird.
II. Aus meiner Arbeit Crelle 153, Satz 14 (Seite 128) folgt, daß die Gleichung
-1 =  12 +
12 +  22 +
22 +  32 in k dann und nur dann lösbar ist, wenn Grad f oder Ordnung
e der Primteiler l von 2 in k gerade ist.1)
32 in k dann und nur dann lösbar ist, wenn Grad f oder Ordnung
e der Primteiler l von 2 in k gerade ist.1)
Da bei der Konstruktion in I. die Ordnung e = 1 wird, weil 2 nicht in der
Diskriminante von kp, also nicht in der von k eingeht, ist also nur noch durch Wahl
von p dafür zu sorgen, daß f gerade wird. Da kp über k von ungeradem
Relativgrad  ist, ist der Grad fp der Primteiler lp von 2 in kp als ungerades
Multiplum von f mit f gleichzeitig gerade oder ungerade. Somit kommt
es nur darauf an, zu bewirken, daß fp gerade wird. Dies fp ist aber der
kleinste Exponent, für den 2fp
ist, ist der Grad fp der Primteiler lp von 2 in kp als ungerades
Multiplum von f mit f gleichzeitig gerade oder ungerade. Somit kommt
es nur darauf an, zu bewirken, daß fp gerade wird. Dies fp ist aber der
kleinste Exponent, für den 2fp  1 mod p wird. Wie man durch Darstellung
von 2 mod p durch eine primitive Wurzel mod p ohne weiteres einsieht, ist
(zufolge (1)) fp dann und nur dann gerade, wenn 2 kein 2n-ter Potenzrest
mod p ist. (Man kann auch direkter so schließen: k ist Klassenkörper zur
Gruppe der 2n-ten Potenzreste mod p über R, also f > 1, d.h. als Teiler
von 2n gerade, dann und nur dann, wenn 2 nicht in jener Gruppe liegt -
Zerlegungsgesetz für den Klassenkörper). Neben (1) ist also auch die Forderung zu
erfüllen:
1 mod p wird. Wie man durch Darstellung
von 2 mod p durch eine primitive Wurzel mod p ohne weiteres einsieht, ist
(zufolge (1)) fp dann und nur dann gerade, wenn 2 kein 2n-ter Potenzrest
mod p ist. (Man kann auch direkter so schließen: k ist Klassenkörper zur
Gruppe der 2n-ten Potenzreste mod p über R, also f > 1, d.h. als Teiler
von 2n gerade, dann und nur dann, wenn 2 nicht in jener Gruppe liegt -
Zerlegungsgesetz für den Klassenkörper). Neben (1) ist also auch die Forderung zu
erfüllen:
 | (2) |
III. Es werde p  1 mod 2n aber nicht notwendig auch p
1 mod 2n aber nicht notwendig auch p  1 mod 2n+1
vorausgesetzt. Dann ist (2) entweder unlösbar oder besitzt gleich 2n inkongruente
Lösungen. Tritt ersteres ein, so besitzt p in R(
1 mod 2n+1
vorausgesetzt. Dann ist (2) entweder unlösbar oder besitzt gleich 2n inkongruente
Lösungen. Tritt ersteres ein, so besitzt p in R( ) keinen Primfaktor 1. Grades;
tritt letzteres ein, so besitzt p in R(
) keinen Primfaktor 1. Grades;
tritt letzteres ein, so besitzt p in R( ) genau 2n verschiedene Primfaktoren 1.
Grades - kurz: p wird in R(
) genau 2n verschiedene Primfaktoren 1.
Grades - kurz: p wird in R( ) “voll-zerlegt”. Das letztere ist wiederum
gleichbedeutend damit, daß p im zugehörigen Galoisschen Körper R(
) “voll-zerlegt”. Das letztere ist wiederum
gleichbedeutend damit, daß p im zugehörigen Galoisschen Körper R( 2n,
2n, ), wo
), wo
 2n eine primitive 2n-te Einheitswurzel ist, voll-zerlegt wird. Die Bedingung (2) kann
also auch so geschrieben werden:
2n eine primitive 2n-te Einheitswurzel ist, voll-zerlegt wird. Die Bedingung (2) kann
also auch so geschrieben werden:
 | (3) |
und zwar unter der Voraussetzung p  1 mod 2n. Diese letztere Voraussetzung besagt
nach der Kreiskörpertheorie, daß p im Kreiskörper R(
1 mod 2n. Diese letztere Voraussetzung besagt
nach der Kreiskörpertheorie, daß p im Kreiskörper R( 2n) voll-zerlegt wird. Die
Bedingung (1) fordert zusätzlich:
2n) voll-zerlegt wird. Die
Bedingung (1) fordert zusätzlich:
 | (4) |
Es kommt also darauf an, die Existenz solcher in R( 2n) voll-zerlegter p
nachzuweisen, die weder in R(
2n) voll-zerlegter p
nachzuweisen, die weder in R( 2n,
2n, ), noch in R(
), noch in R( 2n+1) voll-zerlegt werden, d.h.
die Existenz solcher Primideale 1. Grades p aus R(
2n+1) voll-zerlegt werden, d.h.
die Existenz solcher Primideale 1. Grades p aus R( 2n), für die beides der Fall ist.
Das kommt wieder darauf hinaus, zu zeigen, daß diejenigen p, die entweder in
R(
2n), für die beides der Fall ist.
Das kommt wieder darauf hinaus, zu zeigen, daß diejenigen p, die entweder in
R( 2n,
2n, ) oder in R(
) oder in R( 2n+1) voll-zerlegt werden, zusammen höchstens einen
echten Bruchteil aller p ausmachen. Es bezeichne nun rn den Relativgrad
von
2n+1) voll-zerlegt werden, zusammen höchstens einen
echten Bruchteil aller p ausmachen. Es bezeichne nun rn den Relativgrad
von  über R(
über R( 2n), 2 ist der Relativgrad von
2n), 2 ist der Relativgrad von  über R(
über R( 2n), und es
bezeichne rn den Relativgrad des Kompositums (
2n), und es
bezeichne rn den Relativgrad des Kompositums ( ,
, ) über R(
) über R( 2n). Dann
bilden:
2n). Dann
bilden:
- die in R(
 2n,
2n, ) voll-zerlegten p genau den Bruchteil
) voll-zerlegten p genau den Bruchteil  aller p,
aller p,
- die in R(
 2n,
2n, ) voll-zerlegten p genau den Bruchteil
) voll-zerlegten p genau den Bruchteil  aller p,
aller p,
- die in R(
 2n,
2n, ) und R(
) und R( 2n,
2n, ) voll-zerlegten p genau den Bruchteil
) voll-zerlegten p genau den Bruchteil
 aller p,
aller p,
und folglich die entweder ...oder ...voll-zerlegten p genau den Bruchteil
 +
+  -
- aller p.2)
aller p.2)
Es ist also zu beweisen:
 | (5) |
IV. Der Relativgrad rn ist nicht etwa 2n, sondern
Für n = 1,2 ist das klar, weil  weder zu R(
weder zu R( 2) = R(-1) = R noch zu
R(
2) = R(-1) = R noch zu
R( 22) = R(i) gehört. Für n > 3 gehört aber
22) = R(i) gehört. Für n > 3 gehört aber  zu R(
zu R( 2n), sodaß jedenfalls
rn < 2n-1 ist. Dagegen gehört dann schon
2n), sodaß jedenfalls
rn < 2n-1 ist. Dagegen gehört dann schon  nicht zu R(
nicht zu R( 2n). Wäre das nämlich
der Fall, so gehörte
2n). Wäre das nämlich
der Fall, so gehörte  auch zum reellen Unterkörper (2n-2-ten Grades) von
R(
auch zum reellen Unterkörper (2n-2-ten Grades) von
R( 2n), also (weil dieser auch Galoissch ist) auch der Quotient i =
2n), also (weil dieser auch Galoissch ist) auch der Quotient i =  22 zweier
Konjugierten zu
22 zweier
Konjugierten zu  , was unmöglich. Damit ist die Behauptung über rn bewiesen.
Die Gleichung (5) reduziert sich also auf Bis auf n = 1 ist das ersichtlich schon, ohne rn zu benutzen, einzusehen. Für n = 1
ist rn = 22 als Relativgrad des Kompositums (
, was unmöglich. Damit ist die Behauptung über rn bewiesen.
Die Gleichung (5) reduziert sich also auf Bis auf n = 1 ist das ersichtlich schon, ohne rn zu benutzen, einzusehen. Für n = 1
ist rn = 22 als Relativgrad des Kompositums ( ,
, ), was wieder die
erforderliche Relation ergibt.
), was wieder die
erforderliche Relation ergibt.
Entschuldigen Sie den Kopierstift.3) Es geschieht, damit ich einen Durchschlag
behalte. Legen Sie Wert auf Publikation? Dann können Sie vielleicht eine
kleine Note mit Ihrer Anwendung auf irreduzible Darstellungen aus dem
Vorstehenden zusammenstellen und an die Annalen4) oder Gött[inger] Nachrichten
geben.
Mit besten
Grüßen
Ihr H.
Hasse.
Anmerkungen zum Dokument vom 6.10.1927
1Hier zitiert Hasse diejenige Arbeit Has:1923a , in der er das Lokal-Global-Prinzip für
quadratische Formen beweist, im vorliegenden Fall für die Darstellung von -1 durch die
ternäre quadratische Form x12 + x22 + x32. Die Darstellbarkeit von -1 durch diese Form in
einem Körper K bedeutet, wie Noether geschrieben hatte, den Zerfall der Quaternionenalgebra
über K. Mithin sehen wir hier zum ersten Mal explizit das Lokal-Global-Prinzip für eine
Algebra, nämlich für die Quaternionenalgebra, ausgesprochen. Es dauerte mehr als 4 Jahre,
bis sich herausstellte, dass dieses Lokal-Global-Prinzip in der Tat für jede einfache zentrale
Algebra über einem Zahlkörper gilt. Vgl. Noethers Brief * vom 10. 11. 1931.
2Da Hasse keine Referenz für den benutzten Dichtigkeitssatz für voll zerlegte Primideale
gibt, so konnte er wohl annehmen, dass er Emmy Noether bekannt war. In der Tat handelt es
sich um eine unmittelbare Folge “der für die Klassenkörpertheorie grundlegenden analytischen
Relationen”, wie Hasse in seinem Klassenkörperbericht Has:1930a sagt (Teil II, Kap. V. §24);
dabei meint er das Verhalten der L-Reihen im Punkt s = 1. - Heute sehen wir diesen
Dichtigkeitssatz als Spezialfall des allgemeinen Dichtigkeitssatzes von Tschebotareff, der
1925 in den Mathematischen Annalen Tsc:1925 erschienen ist. Allerdings würde für den
vorliegenden Fall schon der schwächere Dichtigkeitssatz von Frobenius aus dem Jahre 1896
ausreichen Frob:1896 .
3Damals wurden Briefe mit der Hand geschrieben. Und zwar in der Regel mit Tinte und
Federhalter (oder Füllfederhalter). Das eignete sich jedoch nicht dazu, einen Durchschlag
(mit Kohlepapier) anzufertigen. Für diesen Zweck waren im Handel besondere “Kopierstifte”
erhältlich, mit denen man zur Herstellung eines Durchschlags kräftig aufdrücken konnte, die
aber wie die Tintenschrift dokumentenecht waren. Weil also Hasse sich einen Durchschlag
angefertigt hatte, ist dieser Brief erhalten geblieben.
4Hasse hat hier die “Mathematischen Annalen” offenbar deshalb vorgeschlagen, weil er
wusste, dass Emmy Noether dort als inoffizielle Herausgeberin tätig war. “Inoffiziell” bedeutet,
dass ihr Name nicht auf dem Titelblatt der Mathematischen Annalen genannt wurde. Wer
allerdings Bescheid wusste und eine Arbeit aus dem Interessengebiet von Emmy Noether in
den Mathematischen Annalen publizieren wollte, der schickte das Manuskript direkt an sie
nach Göttingen; und wenn Emmy Noether die Arbeit empfehlen konnte, dann schickte sie
diese an Blumenthal, den geschäftsführenden Herausgeber. Als Eingangsdatum erschien in der
publizierten Arbeit der Tag, an dem das Manuskript bei Emmy Noether eingetroffen war. -
Zur Tätigkeit von Emmy Noether als inoffizielle Herausgeberin der Mathematischen Annalen
sagte Hermann Weyl in seiner Gedächtnisrede bei der Totenfeier in Bryn Mawr Wey:1935 :
“Emmy Noether was a zealous collaborator in the editing of the Mathematische Annalen.
That this work was never explicitly recognized may have caused her some pain.” - Der Artikel
von Hasse wurde jedoch nicht in den Mathematischen Annalen publiziert, sondern in den
Sitzungsberichten der Berliner Akademie. Siehe den nachfolgenden Brief * vom 19.10.1927.
 12 +
12 +  22 +
22 +  32 in k notwendig bedingt, muß p- 1 genau durch 2n teilbar sein.
Dann ist ersichtlich auch immer k imaginär und k' reell, letzteres weil k' im
Unterkörper
32 in k notwendig bedingt, muß p- 1 genau durch 2n teilbar sein.
Dann ist ersichtlich auch immer k imaginär und k' reell, letzteres weil k' im
Unterkörper  -ten Grades kp' von k
p enthalten ist. Es ist somit zuerst eine
Primzahl p so zu bestimmen, daß
-ten Grades kp' von k
p enthalten ist. Es ist somit zuerst eine
Primzahl p so zu bestimmen, daß
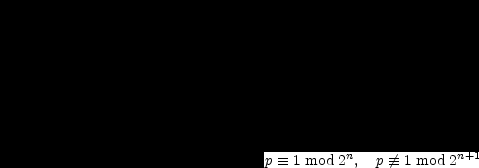
 ist, ist der Grad
ist, ist der Grad 

 ) keinen Primfaktor 1
) keinen Primfaktor 1 ) genau 2
) genau 2 ) “voll-zerlegt”. Das letztere ist wiederum
gleichbedeutend damit, daß
) “voll-zerlegt”. Das letztere ist wiederum
gleichbedeutend damit, daß 
 ), wo
), wo


 ),
),  )
)  über
über  über
über 
 ) über
) über  ) voll-zerlegten
) voll-zerlegten  aller
aller  ) voll-zerlegten
) voll-zerlegten  aller
aller  ) und
) und  ) voll-zerlegten
) voll-zerlegten  aller
aller  +
+ 
 aller
aller 

 weder zu
weder zu  zu
zu  nicht zu
nicht zu  auch zum reellen Unterkörper (2
auch zum reellen Unterkörper (2 , was unmöglich. Damit ist die Behauptung über
, was unmöglich. Damit ist die Behauptung über 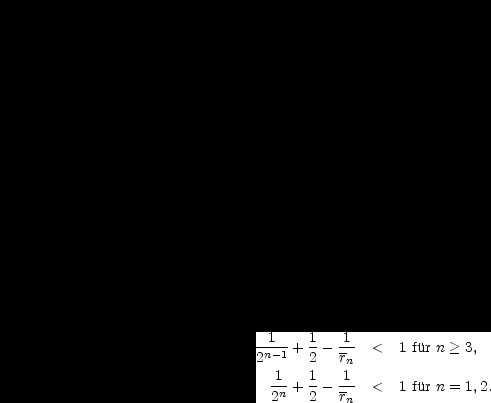

 ), was wieder die
erforderliche Relation ergibt.
), was wieder die
erforderliche Relation ergibt.